Can Matrix Determinant Be Negative

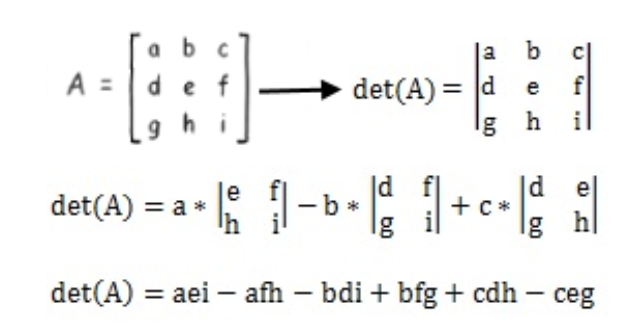
By Bio_Amaris442 01 Sep, 2022 Post a Comment

Each of the quantities in parentheses represents the determinant of a 2 X 2 matrix that is the part of the 3 x 3 matrix remaining when the row and column of the multiplier are. The first method is the general method.

Linear Algebra Ch 2 Determinants 8 Of 48 Example Of Rule 2 The Negative Of A Determinant 3x3 Youtube

Ill just skip that step for now.

. Finding the determinant of a symmetric matrix is similar to find the determinant of the square matrix. The pattern continues for 44 matrices. Now we can see the pattern that the powers follow.

Minus b times the determinant of the matrix that is not in bs row or column. Instead of memorizing the formula directly we can use these two methods to compute the determinant. Also the determinant value can be calculated by using the elements of any row or any column.

Find out the area of the triangle whose vertices are given by A00 B 31 and C 24. If a matrix order is in n x n then it is a square matrix. Determinant of a 44 matrix is a unique number that is also calculated using a particular formula.

Its important when were doing matrix multiplication to confirm that it matters what direction you do the multiplication in. If A is a square matrix then the determinant of the matrix A is. For each entry you want to multiply that entry by the determinant of.

Using determinants we can easily find out the area of the triangle obtained by joining these points using the formula. The determinant of a matrix product is the product of the determinants. If it is negative you can safely skip it.

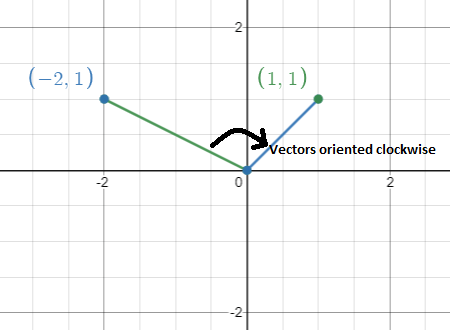
And negative areas are nonsense. Subtracting is actually defined as the addition of a negative matrix. At each power all numbers remain the same except for the element in the second column of the second row which is multiplied by 3.

If the determinant of a matrix is not equal to 0 then it is an invertible matrix as we can find its inverse. Determine if linear transformation corresponding to is orientation-preserving or orientation-reversing. Now we will build the final transform matrix.

There is one caveat to the story. Example To find Area of Triangle using Determinant. If the sign is negative the matrix reverses.

The determinant of a matrix can be either positive negative or zero. Let A be the symmetric matrix and the determinant is denoted as det A or A. A B Multiply by a Constant.

These are the calculations. The determinant of a matrix is defined only for square matrices and this property of the determinant formula makes it unique. To prove it is a special orthogonal matrix you have to show the determinant is 1.

Multiplying Matrices Determinant of a Matrix Matrix Calculator Matrix Index Algebra 2 Index. Minus d times the determinant of the matrix that is not in ds row or column. For instance the continuously.

For 44 Matrices and Higher. We can multiply a matrix by a constant the value 2 in this case. Introduction to Determinant of 4x4 Matrix.

The Jacobian determinant at a given point gives important information about the behavior of f near that point. Determinants can be negative. In this section we will learn the two different methods in finding the determinant of a 3 x 3 matrix.

So here 44 is a square matrix that has four rows and four columns. Plus a times the determinant of the matrix that is not in as row or column. Here it refers to the determinant of the matrix A.

The determinant of matrix is used in Cramers rule which is used to solve the system of equations. The determinant of a matrix is the signed factor by which areas are scaled by this matrix. Also it is used to find the inverse of a matrix.

A determinant is a real number or a scalar value associated with every square matrix. An easy method for calculating 3 X 3 determinants is found by rearranging and factoring the terms given above to get. Be careful to use the translation matrix T and not the transform matrix Tr.

It can work in one direction or another if this matrix is. If m n then f is a function from R n to itself and the Jacobian matrix is a square matrixWe can then form its determinant known as the Jacobian determinantThe Jacobian determinant is sometimes simply referred to as the Jacobian. So were going to calculate up to A 5 to try to figure out the sequence.

Plus c times the determinant of the matrix that is not in cs row or column. A 35 is a power too large to calculate by hand therefore the powers of the matrix must follow a pattern. This method requires you to look at the first three entries of the matrix.

Be extra cautious about the negative sign while calculating the cofactor of the matrix. If we start with an area of 1 and scale it by a negative factor we would end up with a negative area. The determinant of the matrix formed by the basis is negative so it is not right-handed.

We do this by multiplying the translation matrix by the. The determinant of a 3 x 3 matrix A is defined as. But anyway and this works both ways only if were dealing with square matrices.

Linear Algebra Ch 2 Determinants 8 Of 48 Example Of Rule 2 The Negative Of A Determinant 3x3 Youtube